Cho một đơn đồ thị liên thông, vô hướng, có trọng số gồm:

• ~N~ đỉnh - được đánh số từ ~1~ đến ~N~;
• ~M~ cạnh - cạnh ~(u, v, c)~ mô tả đường đi hai chiều trực tiếp giữa hai đỉnh ~u~ và đỉnh ~v~, có chi phí là ~c~;
• ~K~ đỉnh đặc biệt, phân biệt có tính chất như sau: trên đường đi, khi ở một đỉnh đặc biệt có thể di chuyển đến một đỉnh đặc biết bất kỳ trước đó đã đi qua mà không mất chi phí.

Tìm đường đi có tổng chi phí nhỏ nhất đi qua toàn bộ các đỉnh đặc biệt (đường đi có thể xuất phát từ một đỉnh bất kì).

INPUT

• Dòng đầu tiên gồm ba số nguyên dương ~N, M~ và ~K \ (2\le K\le N; \ N, M\le 10^5)~ mô tả số lượng đỉnh, số lượng cạnh và số lượng đỉnh đặc biệt;
• Dòng thứ hai gồm ~K~ số nguyên dương ~S \ (S \le N)~ mô tả các đỉnh đặc biệt;
• ~M~ dòng sau, mỗi dòng gồm ba số nguyên dương ~u, v, c \ (u, v\le N; \ c\le 10^9)~ mô tả các cạnh của đồ thị.

OUTPUT

Một số nguyên duy nhất là tổng chi phí nhỏ nhất của đường đi thoả mãn yêu cầu.

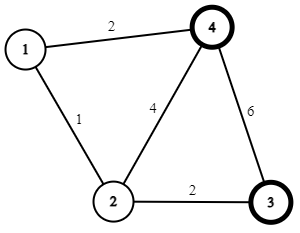
SAMPLE INPUT 1

4 5 2
4 3
1 2 1
2 3 2
4 1 2
4 2 4
3 4 6

SAMPLE OUTPUT 1

5

Có thể đi theo đường đi: ~4 \rightarrow 1 \rightarrow 2 \rightarrow 3~

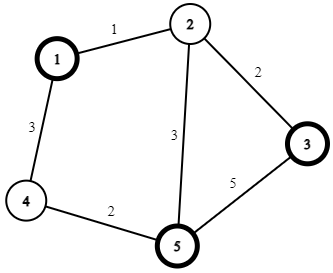
SAMPLE INPUT 2

5 6 3
5 1 3
1 2 1
2 3 2
4 1 3
4 5 2
5 2 3
3 5 5

SAMPLE OUTPUT 2

7

Có thể đi theo đường đi: ~1 \rightarrow 2 \rightarrow 3 \rightarrow 1\rightarrow 2\rightarrow 5~

SUBTASKS

• Có ~20\%~ số test ứng với ~20\%~ số điểm thoả mãn: ~K=2; \ N\le 10^4~;
• ~15\%~ số test khác ứng với ~15\%~ số điểm thoả mãn: ~K=5; \ N\le 10^4~;
• ~15\%~ số test khác ứng với ~15\%~ số điểm thoả mãn: ~K=N~;
• ~15\%~ số test khác ứng với ~15\%~ số điểm thoả mãn: ~N, M\le 10^3~;
• ~20\%~ số test khác ứng với ~20\%~ số điểm thoả mãn: ~M=N-1~;
• ~15\%~ số test khác ứng với ~15\%~ số điểm không có ràng buộc gì thêm.