Cho một cây gồm ~N~ đỉnh được đánh số từ ~1~ đến ~N~, trong đó đỉnh ~1~ là gốc của cây. Tất cả đỉnh trên đường đi từ đỉnh ~1~ đến đỉnh ~u~ được gọi là tổ tiên của đỉnh ~u~. Mỗi đỉnh đều có hai loại trọng số, đỉnh thứ ~i~ có trọng số đỉnh là ~a_i~ và trọng số tổ tiên là ~b_i~.

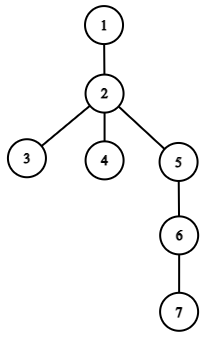
Tổ tiên chung gần nhất của một tập đỉnh là đỉnh chung đầu tiên của các đỉnh khi đi về đỉnh gốc ~1~ (nếu tập hợp gồm ~1~ đỉnh thì tổ tiên chung gần nhất là chính đỉnh đó). Ví dụ, như hình dưới, tổ tiên chung gần nhất của tập hợp đỉnh ~\{3, 7\}~ là đỉnh ~2~; tổ tiên chung gần nhất của tập hợp đỉnh ~\{4, 7, 1\}~ là đỉnh ~1~.

Xét một tập hợp gồm ~k \ (0 \lt k \le N)~ đỉnh phân biệt bất kì ~\{u_1, u_2, \dots, u_k\}~. Gọi ~p~ là tổ tiên chung gần nhất của ~k~ đỉnh. Khi đó giá trị của tập đỉnh này được tính bằng công thức: ~a_{u_1} \times a_{u_2} \times \dots \times a_{u_k} \times b_p~. Vậy một cây ~N~ đỉnh sẽ có ~2^N - 1~ tập đỉnh phân biệt.

Hãy tính tổng giá trị của tất cả các tập đỉnh có thể tạo ra.

INPUT

• Dòng đầu tiên chứa số nguyên dương ~N \ (N \le 10^6)~ là số đỉnh của cây;
• Dòng thứ hai chứa ~N~ số nguyên dương ~a_1, a_2, \dots, a_N \ (a_i \le 10^9; \ 1\le i\le N)~ mô tả trọng số đỉnh của các đỉnh tương ứng từ đỉnh ~1~ đến đỉnh ~N~;
• Dòng thứ ba chứa ~N~ số nguyên dương ~b_1, b_2, \dots, b_N \ (b_i \le 10^9; \ 1\le i\le N)~ mô tả trọng số khi nó là tổ tiên của các đỉnh tương ứng từ đỉnh ~1~ đến đỉnh ~N~;
• ~N - 1~ dòng tiếp theo, mỗi dòng chứa hai số nguyên dương ~u, v \ (u, v\le N)~ mô tả cạnh của cây.

OUTPUT

Gồm một số nguyên duy nhất là kết quả của bài toán, vì kết quả có thể rất lớn nên in ra phần dư của kết quả khi chia cho ~10^9+7~.

SAMPLE INPUT

3
1 1 2
2 1 2
1 2
1 3

SAMPLE OUTPUT

21

• Tập đỉnh ~\{1\}~ có giá trị: ~2~
• Tập đỉnh ~\{2\}~ có giá trị: ~1~
• Tập đỉnh ~\{3\}~ có giá trị: ~4~
• Tập đỉnh ~\{1, 2\}~ có giá trị: ~2~
• Tập đỉnh ~\{1, 3\}~ có giá trị: ~4~
• Tập đỉnh ~\{2, 3\}~ có giá trị: ~4~
• Tập đỉnh ~\{1, 2, 3\}~ có giá trị: ~4~

~\Rightarrow~ Tổng là: ~21~

SUBTASKS

• Có ~20\%~ số test ứng với ~20\%~ số điểm có ~N \le 15~ và cây có dạng đường thẳng: đỉnh ~1~ nối với đỉnh ~2~, đỉnh ~2~ nối với đỉnh ~3~, ..., đỉnh ~N-1~ nối với đỉnh ~N~;
• ~20\%~ số test khác ứng với ~20\%~ số điểm có ~N\le 15~;
• ~20\%~ số test khác ứng với ~20\%~ số điểm có cây có dạng đường thẳng: đỉnh ~1~ nối với đỉnh ~2~, đỉnh ~2~ nối với đỉnh ~3~, ..., đỉnh ~N-1~ nối với đỉnh ~N~;
• ~20\%~ số test khác ứng với ~20\%~ số điểm có mọi trọng số đỉnh của các đỉnh đều là ~1~;
• ~20\%~ số test khác ứng với ~20\%~ số điểm không có ràng buộc gì thêm.