Chữ số tận cùng của một số là chữ số cuối cùng của số đó.

Ví dụ: Số ~268~ có chữ số tận cùng là ~8~; số ~7~ có chữ số tận cùng là ~7~.

Yêu cầu: Cho hai số nguyên dương ~a, b~. Hãy tìm chữ số tận cùng của ~a^b~

Input

Một dòng duy nhất ghi hai số nguyên dương lần lượt là ~a, b~. Hai số cách nhau một dấu cách.

Output

Một số nguyên duy nhất là chữ số tận cùng tìm được

Sample Input

3 4

Sample Output

1

Giải thích

~3^4~ = ~3 \times 3 \times 3 \times 3~ ~=~ ~81~

An đang ngồi học lập trình nhưng có một bài làm An bối rối, bạn hãy giúp An giải quyết bài toán đó nhé.

Bài toán như sau: Cho dãy số gồm ~n~ số nguyên không âm ~a_1, a_2,..., a_n~. Hãy tìm số chính phương nhỏ nhất không xuất hiện trong dãy số đã cho.

Biết rằng: Số chính phương là số tự nhiên mà có thể viết dưới dạng bình phương của một số tự nhiên khác.

Ví dụ: ~0, 1, 4, 9, 16, 25,...~ là các số chính phương, còn các số: ~2, 3, 5,...~ không là số chính phương

Input

Dòng đầu tiên chứa số nguyên ~n~ ~(1 \le n \le 10^6)~;

Dòng thứ hai chứa ~n~ số nguyên ~a_1, a_2, ..., a_n~ ~(0 \le a \le 10^{12}, i = 1, 2, ..., n)~, các số cách nhau một dấu cách.

Output

Một số nguyên duy nhất là kết quả của bài toán

Subtask

• Subtask 1: ~50\%~ số test đầu tiên ~n \le 10 ^ 1 0 \le a_{i} \le 10 ^ 4~
• Subtask 2: ~30\%~ số test tiếp theo ~10 ^ 3 < n \le 10 ^ 6 0 \le a_{i} \le 10 ^ 6~
• Subtask 3: ~20\%~ số test cuối cùng ~0 \le a_{i} \le 10 ^ {12}~

Sample Input

8 
0 3 4 2 1 4 16 25

Sample Output

9

Trong cuộc thi Robocon tỉnh Bắc Giang lần 2, vòng loại cuộc thi được tổ chức trên phân mềm giả lập Robosim. Phần thi thể hiện kỹ năng thiết kế, tư duy lập trình của các đội thi. Một sa bàn có kích thước ~M \times N~ (~M~ là số hàng, ~N~ là số cột) được chia thành các lưới ô vuông đơn vị có kích thước ~1 \times 1~. Trên sa bàn được bố trí các nhiệm vụ mà Robot phải thực hiện. Để thuận lợi cho việc lập trình Robot thực thi các nhiệm vụ trên sa bàn, đội thi của Nam đã thực hiện phân tích, mã hóa vị trí của các nhiệm vụ và lưu trữ trong các tập tin văn bản với quy ước như sau:

Khu vực chứa nhiệm vụ được mã hóa thành các hình chữ nhật có kích thước ~1 \times k~ ~(k <= N)~ chứa các số khác ~0~, khu vực không chứa nhiệm vụ được mã hóa bằng số ~0~. Biết rằng các khu vực chứa nhiệm vụ không liền sát nhau. Độ khó của một nhiệm vụ được xác định bằng tổng các số trong các ô của khu vực đặt nhiệm vụ đó.

Ví dụ: Sa bàn dưới đây có kích thước ~3 \times 10~ gồm ~5~ khu vực chứa các nhiệm vụ. Độ khó của từng nhiệm vụ là: ~4 = 1 + 3~, ~11 = 6 + 4 + 1~, ~8 = 4 + 4~, ~9 = 9~, ~5 = 2 + 3~

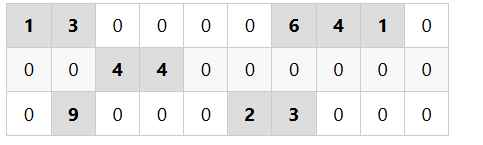
Yêu cầu: Hãy đếm số lượng các khu vực chứa nhiệm vụ có độ khó là một số nguyên tố.

Input

Dòng đầu tiên chứa hai số nguyên dương ~M, N (1 \le M, N \le 10 ^ 5)~

~M~ dòng tiếp theo chứa ~N~ số nguyên ~a_i~ ~( 0 \le a_{i} \le 10 ^ 8 , i = 1, 2 ,...,N)~ , các số cách nhau một dấu cách.

Output

Một dòng duy nhất là số lượng khu vực chứa nhiệm vụ có độ khô là một số nguyên tố.

Subtask

• Subtask 1: Có ~50\%~ số test có số các chữ số của ~M \le 50~, ~N \le 50~, ~a_{i} \le 10 ^ 2~
• Subtask 2: Có ~25\%~ số test có ~M \le 5~, ~N \le 100~, ~a_{i} \le 10 ^ 8~
• Subtask 3: Có ~25\%~ số test có ~M \le 10 ^ 5~, ~N \le 500~, ~a_{i} \le 10 ^ 4~

Sample Input

3 10 
1 3 0 0 0 0 6 4 1 0 
0 0 0 4 3 0 0 0 0 0 
0 9 0 0 0 0 2 3 0 0

Sample Output

3

Giải thích:

• KV1: Độ khó ~= 1+3 = 4~ không là số nguyên tố;
• KV2: Độ khó ~= 6+4+1=11~ là số nguyên tố;
• KV3: Độ khó ~= 4 + 3 = 7~ là số nguyên tố;
• KV4: Độ khó ~= 9~ không là số nguyên tố;
• KV5: Độ khó ~= 2+3 = 5~ là số nguyên tố;

~\longrightarrow~ Số khu vực chứa NV có độ khó là một số nguyên tố: ~3~ khu vực

Một ngày rảnh rỗi, Nam chơi trò chơi với những con số. Nam lấy một số tự nhiên ~N~ rồi thực hiện biến đổi thành số mới. Với mỗi cách biến đổi Nam xóa đi một số chữ số liên tiếp của ~N~ (nhưng không xóa hết) Nam nhận được một số mới, nếu số ~N~ được chia thành ~2~ phần thì số mới được ghép từ hai phần này và giữ nguyên thứ tự.

Yêu cầu: Hãy đếm các cách biến đổi như trên để số ~N~ mới sau khi biến đổi chia hết cho ~3~.

Lưu ý: Thao tác xóa tại hai vị trí khác nhau sẽ tạo ra hai cách biến đổi khác nhau. Số ~N~ giữ nguyên được coi là một cách biến đổi.

Input

Một dòng duy nhất là số nguyên ~N~ ~(1 \le |N| \le 10^5~, ~|N|~ số lượng chữ số của ~N~ ~)~

Output

In ra số cách xoá tìm được

Subtask

• Subtask 1: Có ~50\%~ số test có số các chữ số của ~N \le 300~
• Subtask 2: Có ~25\%~ số test có số các chữ số của ~N \le 10 ^ 4~
• Subtask 3: Có ~25\%~ số test có số các chữ số của ~N \le 10 ^ 5~

Sample Input 1

2001

Sample Output 1

4

Sample Input 2

160300

Sample Output 2

5

Giải thích

• Trong test 1: Các số mới là: ~2001; 201; 201; 21~

• Trong test 2: Các số mới là: ~60300; 0300; 300; 00; 0~