Hướng dẫn giải của duong3982oj Contest 02 - Dãy con tăng dài nhất
Nộp một lời giải chính thức trước khi tự giải là một hành động có thể bị ban.
Tác giả:
Mấu chốt của bài này là nhận ra ta có thể dp như bài dãy con tăng dần bình thường 😁
Ta gọi ~dp[r]~ là độ dài đoạn con tăng dài nhất kết thúc ở ~r~
Bây giờ ta sẽ chứng minh một điều là : Với mỗi con ~r~ ta sẽ chỉ được ghép với các đầu mút ~r'~ khác bé hơn ~r~
Ta sẽ chứng minh bằng phản chứng như sau
Chứng minh :
TH1 : đoạn ~[l', r']~ giao 1 phần với đoạn ~[l,r]~
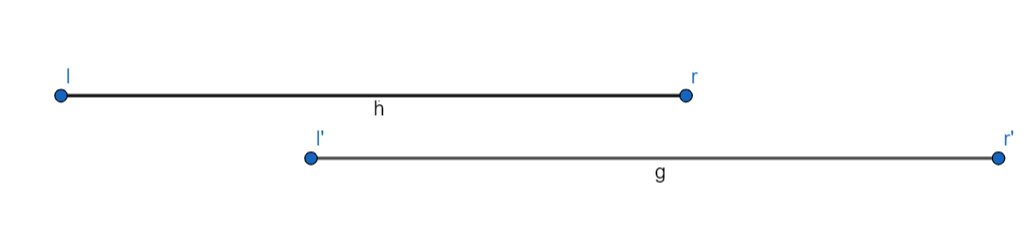
Dễ thấy ta sẽ ko chọn như thế này vì đoạn ~[l,r]~ chắc chắn sẽ dài hơn
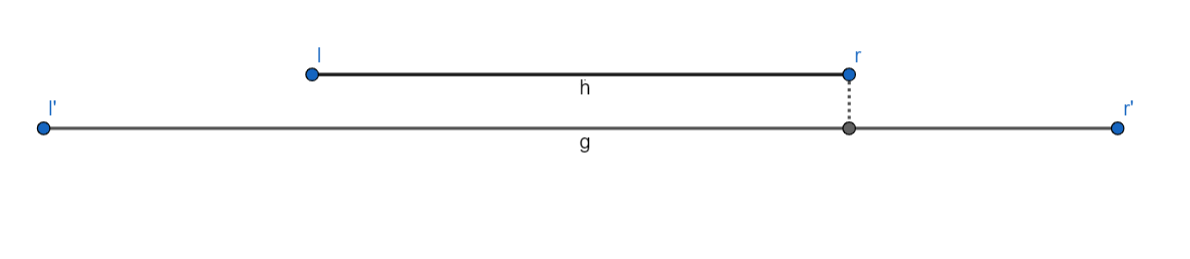
TH2 : đoạn ~[l', r']~ bao hoàn toàn đoạn ~[l,r]~
Mặc dù đúng là đoạn ~[l',r]~ là đoạn dài nhất kết thúc ở ~r~ nhưng mà liệu nó có thực sự tối ưu?
Dễ thấy, đoạn ~[l',r']~ vẫn là đoạn dài nhất trong trường hợp này vậy nếu ta thực sự muốn chọn đoạn ~[l',r]~ cho ~dp[r]~ ta sẽ phải tìm ra trường hợp mà nó sẽ đóng góp cho ~1~ đoạn dài hơn ~[l',r']~
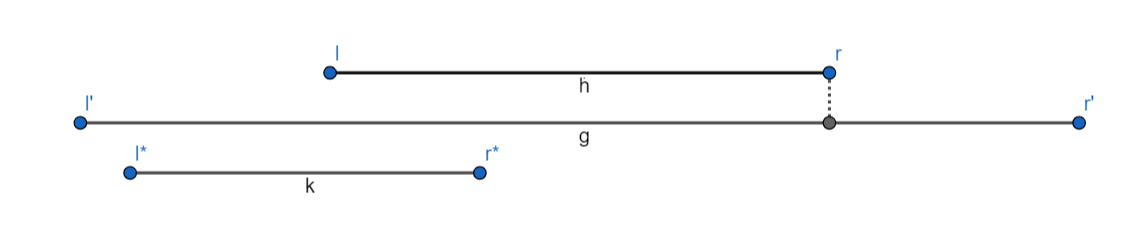
Ta sẽ gọi đoạn đó là ~[l*,r*]~, đoạn này có những trường hợp như sau
- Tất cả trường hợp với ~[l*,r*]~ nhưng ~l* < l' < l~
Cũng giống TH1, ở đây ta mà nối thì sẽ luôn ra 1 đoạn ~<~ ~[l*,r*]~ nên nó sẽ ko đóng góp gì cho ~dp[r*]~
- ~[l*,r*]~ có ~r* < r~
Dễ thấy trường hợp này nó chả đóng góp được gì cho đáp án cả 😁
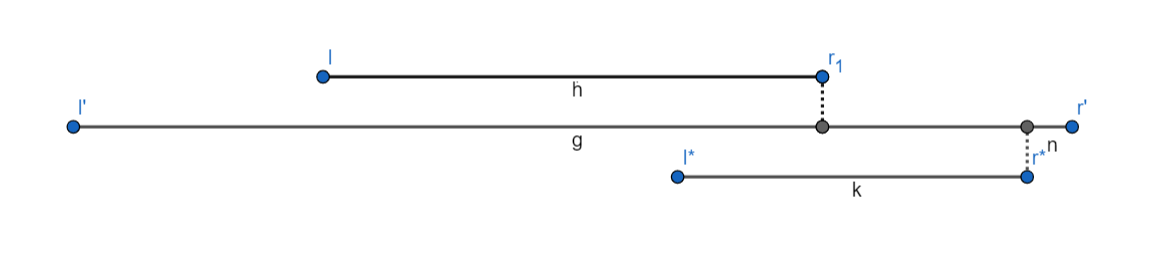
- ~[l*,r*]~ có ~r' > r* > r~
Tương tự trường hợp này nó sẽ bỏ qua đoạn ~[l',r]~ mà dù nó có dùng thì đoạn ~[l',r']~ vẫn là đoạn dài nhất
- ~[l*,r*]~ có ~r* > r'~
Trường hợp này ta nhận ra 1 điều là chả dại gì mà chọn đoạn ~[l',r]~ để nối thêm mà thay vào đó sẽ nối bằng đoạn ~[l',r']~ từ đó ra được đoạn ~[l',r*]~
Từ đó ta suy ra được điều phải chứng minh 😙, đến đây thì sẽ chỉ còn là 1 bài dp tối ưu bằng segment tree cơ bản thôi.
~O(nlog_{2}n)~
Ta sẽ for từng đoạn ~[l,r]~ theo thứ tự được thêm vào vào dùng segment tree để tìm ra đáp án
Đầu tiên ~dp[r] = max(dp[r], r-l+1)~
TH1 : ~r' < l~
Với trường hợp này thì ta sẽ chỉ làm ~dp[r] = max(dp[r], dp[r'] + r-l+1)~
TH2 : ~l < r' < r~
Với trường hợp này thì ta sẽ làm ~dp[r] = max(dp[r], dp[r'] + r-r')~
Và ta sẽ tạo... 2 cái segment tree để quản lý cả 2 trường hợp này 😅 (Mình nghĩ cách này hơi phiền nên mình nghĩ sẽ có bạn nghĩ ra cách khác tốt hơn)
Segment tree 1 đơn giản chỉ lưu ~dp[r]~ cho mỗi con ~r~ Segment tree 2 sẽ lưu ~dp[r] - r~ cho mỗi con ~r~
Lúc này, với mỗi con ~r~ ta sẽ query max trong 1 đoạn :
- Đoạn 1 sẽ dùng segment tree 1 trong ~[1,l-1]~
- Đoạn 2 sẽ dùng segment tree 2 trong ~[l,r]~
Xong rồi thì ta sẽ point update cho 2 con segment tree ở vị trí r thôi 😋
LƯU Ý : Nếu ~dp[x] = dp[y]~ hay ~dp[x] - x = dp[y] - y~ thì chọn con ~x~ hoặc ~y~ bé hơn vì nó sẽ cho mình nhiều cơ hội hơn
Code mẫu
#include <bits/stdc++.h>
using namespace std;
#define int long long
pair<int,int> a[100005];
int dp[200005];
vector<int> v;
int t[800005];
int t2[800005];
int maximize(int x, int y){
if(x == 0) return y;
if(y == 0) return x;
if(dp[x] > dp[y]) return x;
else if(dp[x] < dp[y]) return y;
else{
if(v[x-1] < v[y-1]) return x;
else return y;
}
}
void update(int v, int tl, int tr, int pos, int val){
if(tl == tr) t[v] = tl;
else{
int tm = (tl+tr)/2;
if(pos <= tm) update(v*2,tl,tm,pos,val);
else update(v*2+1,tm+1,tr,pos,val);
t[v] = maximize(t[v*2],t[v*2+1]);
}
}
int query(int v, int tl, int tr, int l, int r){
if(l > r) return 0;
if(l > tr || r < tl) return 0;
if(l <= tl && tr <= r) return t[v];
int tm = (tl+tr)/2;
return maximize(query(v*2,tl,tm,l,r),query(v*2+1,tm+1,tr,l,r));
}
int maximize2(int x, int y){
if(x == 0) return y;
if(y == 0) return x;
if(dp[x] - v[x-1] > dp[y] - v[y-1]) return x;
else if(dp[x] - v[x-1] < dp[y] - v[y-1]) return y;
else{
if(v[x-1] < v[y-1]) return x;
else return y;
}
}
void update2(int v, int tl, int tr, int pos, int val){
if(tl == tr) t2[v] = tl;
else{
int tm = (tl+tr)/2;
if(pos <= tm) update2(v*2,tl,tm,pos,val);
else update2(v*2+1,tm+1,tr,pos,val);
t2[v] = maximize2(t2[v*2],t2[v*2+1]);
}
}
int query2(int v, int tl, int tr, int l, int r){
if(l > r) return 0;
if(l > tr || r < tl) return 0;
if(l <= tl && tr <= r) return t2[v];
int tm = (tl+tr)/2;
return maximize2(query2(v*2,tl,tm,l,r),query2(v*2+1,tm+1,tr,l,r));
}
signed main(){
ios_base::sync_with_stdio(0);
cin.tie(0);
int n;
cin >> n;
for(int i = 1; i <= n; i++){
cin >> a[i].first >> a[i].second;
v.push_back(a[i].first);
v.push_back(a[i].second);
}
sort(v.begin(),v.end());
v.erase(unique(v.begin(),v.end()), v.end());
for(int i = 1; i <= n; i++){
int l = a[i].first, r = a[i].second;
a[i].first = lower_bound(v.begin(),v.end(),l) - v.begin() + 1;
a[i].second = lower_bound(v.begin(),v.end(),r) - v.begin() + 1;
}
dp[0] = -1e17;
for(int i = 1; i <= n; i++){
int l = a[i].first, r = a[i].second;
dp[r] = max(dp[r], v[r-1]-v[l-1]+1);
int k1 = query(1,1,v.size(),1,l-1);
int k2 = query2(1,1,v.size(),l,r-1);
if (k1 > 0){
dp[r] = max(dp[r], dp[k1] + v[r-1] - v[l-1] + 1);
}
if (k2 > 0){
dp[r] = max(dp[r], dp[k2] + v[r-1] - v[k2-1]);
}
update(1,1,v.size(),r,1);
update2(1,1,v.size(),r,1);
//cout << dp[r] << ' ' << r << ' ' << v[r-1] << endl;
}
int ans = 0;
for(int i = 1; i <= v.size(); i++) ans = max(ans,dp[i]);
cout << ans;
return 0;
}





Bình luận