Có một lưới thành phố kích thước ~n \times m~, mỗi thành phố được kết nối bởi các con đường một chiều, biểu diễn trong một ma trận ~n \times m~ như sau:

• >: Đường đi sang phải, nghĩa là từ thành phố ~(i,j)~ chỉ có thể đi đến thành phố ~(i,j+1)~.

• <: Đường đi sang trái, nghĩa là từ thành phố ~(i,j)~ chỉ có thể đi đến thành phố ~(i,j-1)~.

• ^: Đường đi lên trên, nghĩa là từ thành phố ~(i,j)~ chỉ có thể đi đến thành phố ~(i-1,j)~.

• v: Đường đi xuống dưới, nghĩa là từ thành phố ~(i,j)~ chỉ có thể đi đến thành phố ~(i+1,j)~.

~Zinno~ muốn đi từ ô ~(1,1)~ đến ô ~(n,m)~, anh ấy chỉ có thể đi theo các con đường một chiều đã có sẵn. Tuy nhiên, có thể các con đường một chiều này có thể không cho phép anh ấy đi từ ô ~(1,1)~ đến ô ~(n,m)~. Vì vậy, ~Zinno~ có thể thay đổi hướng của một số con đường để tìm được đường đi, nhưng anh ấy chỉ có thể thay đổi hướng của con đường tại một thành phố duy nhất mỗi lần.

Câu hỏi là: ~Zinno~ có cần thay đổi hướng của bất kỳ con đường nào không? Nếu có, cần thay đổi tại bao nhiêu thành phố?

Input

Dòng đầu tiên là 2 số nguyên ~n~ và ~m~ ~(1 \le n,m \le 1000, n \times m \le 2 \times 10^5)~

~n~ dòng tiếp theo,mỗi dòng là ~1~ xâu gồm ~m~ kí tự chỉ bao gồm > , < , ^ , v

Output

Dòng đầu tiên in ra YES nếu cần thay đổi,NO nếu không

In ra dòng tiếp theo nếu dòng trên là YES, số lượng thành phố cần thay đổi đường

Sample Input

4 4
>>>>
<<<<
>>>>
<<<<

Sample Output

YES
3

Giải thích

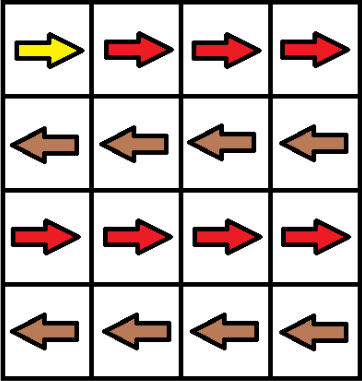
Thay đổi ô ~(1,4)~ thành v,thay đổi ô ~(2,1)~ thành v,thay đổi ô ~(3,4)~ thành v