Nam và Bắc là đôi bạn thân, nhưng luôn ganh đua nhau trong học tập, đặc biệt là môn Toán. Hôm nay Nam thách thức một bài toán hơi khó đối với Bắc. Nhận thấy bài toán có thể dùng máy tính để tìm ra nghiệm, Bắc nhờ bạn lập trình giải giúp bài toán đố của Nam.

Yêu cầu: Cho trước hai số nguyên dương ~a~ và ~b~, hãy tìm số nguyên dương ~x~ nhỏ nhất sao cho ~a+x~ chia hết cho ~b~, đồng thời ~b+x~ chia hết cho ~a~.

Input

• Một dòng chứa hai số nguyên ~a~ và ~b~ (~1 \le a,b, \le 10^9~).

Output

• Một dòng chứa số nguyên dương ~x~ tìm được.

Sample Input

6 10

Sample Output

14

Một bản đồ hình vuông kích thước ~n \times n~ được chia thành lưới ô vuông. Người ta lần lượt đặt vào mỗi ô vuông của lưới các ô vuông. Người ta lần lượt đặt vào mỗi ô vuông của lưới một số tiền thưởng là các số nguyên liên tiếp bắt đầu từ ~1~ đến ~n^2~ đi theo dạng dích dắc bắt đầu từ ô ~(1,1)~ như hình minh họa với ~m = 6~.

Một robot xuất phát tại ô ~(x,y)~ của lưới. Mỗi lần nhận tín hiệu điều khiển được mô tả bởi các kí tự {E,W,S,N}, robot di chuyển sang ô kề cạnh tương ứng theo hướng Đông, Tây, Nam, Bắc.

Khi di chuyển đến ô nào, robot sẽ lấy hết số tiền thưởng tại ô đó, nghĩa là ô này không còn tiền thưởng.

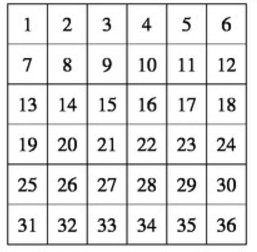
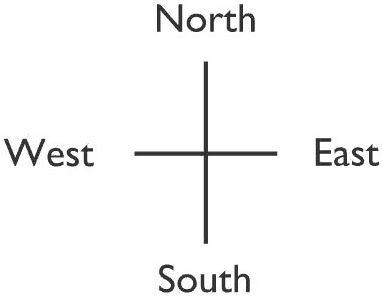
Yêu cầu: Cho dãy lệnh điều khiển robot. Cho biết tổng số tiền thưởng mà robot nhận được sau khi kết thúc hành trình.

Input

• Dòng thứ nhất chứa ba số nguyên ~n,x,y~ là kích thước của hình vuông và vị trí ban đầu của robot (~1 \le n \le 10^6, 1 \le x,y \le n~).
• Dòng tiếp theo chứa các xâu gồm các kí tự {E,W,S,N} có độ dài không quá ~5 \times 10^5~ tương ứng với dãy lệnh điều khiển robot. Dữ liệu đảm bảo robot không vượt ra ngoài bảng.

Output

• Một dòng chứa một số nguyên là tổng số tiền thưởng của robot.

Sample Input

6 1 1
SSSSSNNEEENWSW

Sample Output

136

Để chuẩn bị cho giải đấu sắp tới, huấn luyện viên (HLV) lên giáo án tập luyện để nâng cao kĩ năng thi đấu cho ~n~ vận động viên (VĐV). Ban đầu VĐV thứ ~i~ có kĩ năng thi đấu ~a_{i}~.

HLV chuẩn bị ~m~ bài tập, bài tập thứ ~j~ có độ khó ~b_{j}~. HLV chỉ định trình tự tập luyện từng bài cho từng VĐV tùy vào kĩ năng thi đấu và mỗi bài tập chỉ tập tối đa ~1~ lần để tránh nhàm chán. Để thực hiện bài có độ khó ~x~, VĐV phải có kĩ năng thi đấu không nhỏ hơn ~x~ và sau khi hoàn thanh, kĩ năng thi đấu của VĐV tăng thêm ~x~ đơn vị. Để đánh giá tính hiệu quả của giáo án, HLV cần biết kĩ năng thi đấu cao nhất của từng VĐV đạt được sau đợt tập huấn.

Yêu cầu: Cho kĩ năng thi đấu ban đầu của ~n~ VĐV và độ khó của ~m~ bài tập. Hãy cho biết kĩ năng thi đấu cao nhất của từng VĐV sau đợt tập huấn.

Input

• Dòng thứ nhất chứa hai số nguyên ~n,m~ lần lượt là số lượng VĐV và số bài tập (~1 \le n,m \le 5 \times 10^5~).
• Dòng thứ hai chứa ~n~ số nguyên ~a_{1}, a_{2}, ..., a_{n}~ là kĩ năng thi đấu của các VĐV (~1 \le a_{i} \le 10^9~).
• Dòng thứ ba chứa ~m~ số nguyên ~b_{1}, b_{2}, ..., b_{m}~ là độ khó của các bài tập (~1 \le b_{j} \le 10^9~).

Output

• Một dòng chứa một dãy gồm ~n~ số nguyên, số thứ ~i~ là kĩ năng thi đấu cao nhất của VĐV thứ ~i~ sau đợt tập huấn.

Sample Input

5 4
4 6 1 2 9
7 31 2 15

Sample Output

6 30 1 4 64

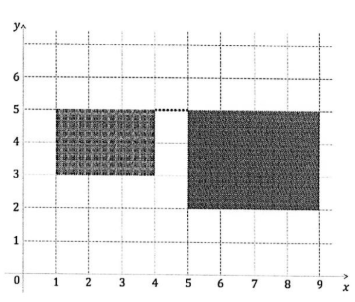
Một dự án xây dựng cơ sở mới cho Trường PTNK gồm hai tòa nhà cao tầng. Trên bảng vẽ, nhìn từ trên xuống các tòa nhà có thể xem như các hình chữ nhật có cạnh song song với hệ trục tọa độ và không giao nhau. Mỗi hình chữ nhật được xác định bởi tọa độ góc trái dưới và phải trên. Hình thứ nhất có tọa độ góc trái dưới ~(x_{1}, y_{1})~ và phải trên ~(x_{2}, y_{2})~. Hình thứ hai có tọa độ góc trái dưới ~(x_{3}, y{3})~ và phải trên ~(x_{4}, y_{4})~. Tọa độ đều là các số nguyên có giá trị tuyệt đối không vượt quá ~10^6~.

Để tiện lợi cho việc đi lại giữa hai tòa nhà và tránh được mưa nắng, nhà trường đề nghị làm một đường mái che nối hai toàn nhà. Trên bản vẽ, đường mái che là một đoạn thẳng nối một điểm trên cạnh hình chữ nhật này đến một điểm trên cạnh của hình chữ nhật còn lại. Để tiết kiệm chi phí, nhà trường cần tìm phương án làm đường mái che sao cho độ dài của đoạn thẳng tương ứng là nhỏ nhất có thể.

Yêu cầu: Cho trước ~8~ giá trị ~x_{1}, y_{1}, x_{2}, y_{2}, x_{3}, y_{3}, x_{4}, y_{4}~. Hãy tính bình phương độ dài ngắn nhất của đoạn cần làm mái che.

Input

• Một dòng chứa ~8~ số nguyên ~x_{1}, y_{1}, x_{2}, y_{2}, x_{3}, y_{3}, x_{4}, y_{4}~ có giá trị tuyệt đối không vượt quá ~10^6~.

Output

• Một dòng chứa ~1~ số nguyên là bình phương độ dài mái che tìm được.

Sample Input

1 3 4 5 5 2 9 5

Sample Output

1

Giải thích: