duong3982oj Contest 01
duong3982oj Contest 01 - Lũy thừa
Nộp bàiPoint: 250
Cho hai số nguyên dương ~A~ và ~B~. Hãy tính ~A^B~.
Vì kết quả có thể rất lớn, nên nếu kết quả có nhiều hơn ~6~ chữ số, bạn chỉ cần in ra ~6~ chữ số cuối cùng của kết quả. Nếu kết quả có ít hơn hoặc bằng ~6~ chữ số, bạn chỉ cần in ra kết quả.
INPUT
Hai số nguyên dương duy nhất ~A~ và ~B~ (~A, B \le 10^6~) trên một dòng.
OUTPUT
Kết quả bài toán.
SAMPLE INPUT 1
27 9
SAMPLE OUTPUT 1
484987
duong3982oj Contest 01 - Cuốn sách
Nộp bàiPoint: 500
Đây có thể là một bài toán vô cùng kinh điển khi các bạn học chương trình Toán 1:
Cho một cuốn sách có 100 trang. Hỏi ta cần bao nhiêu chữ số để đánh số quyển sách này?
Bài toán này, sẽ là bài toán tổng quát hơn của bài trên.
Yêu cầu: Cho ~T~ truy vấn gồm hai dạng sau:
1 x: Cho một cuốn sách có ~n~ trang. Hỏi ta cần bao nhiêu chữ số để đánh số quyển sách này?
2 x: Cho một cuốn sách có ~n~ chữ số. Hỏi cuốn sách này có bao nhiêu trang? Nếu cuốn sách này không hợp lệ, in ra ~-1~.
Biết rằng, các trang trong cuốn sách được đánh số từ ~1~.
INPUT
Dòng đầu tiên chứa số nguyên dương ~T~ (~1 \le T \le 1000~).
~T~ dòng tiếp, mỗi dòng gồm hai số nguyên dương ~type~ và ~x~ (~type \le 2~, ~x \le 10^9~).
OUTPUT
~T~ dòng, là kết quả của các truy vấn tương ứng.
SAMPLE INPUT 1
2
1 100
2 192
SAMPLE OUTPUT 1
192
100
duong3982oj Contest 01 - Bảng đẹp
Nộp bàiPoint: 1000
Cho bảng ~a~ kích thước ~m \times n~. Dòng thứ ~i~ cột ~j~ của bảng có giá trị ~a_{i, j}~. Một bảng con của bảng ~a~ được xác định bởi góc trái trên ~(u, v)~ và góc phải dưới ~(p, q)~ gồm các ô ~(i, j)~ thỏa mãn ~u \le i \le p~ và ~v \le j \le q~.
Một bảng con được định nghĩa là "đẹp" khi tổng tất cả giá trị trong bảng đó không vượt quá ~k~ cho trước.
Yêu cầu: Tìm bảng đẹp là bảng vuông con có kích thước lớn nhất của bảng ~a~.
Kích thước của bảng vuông được định nghĩa là kích thước cạnh.
INPUT
Dòng đầu tiên chứa ba số nguyên dương ~m~, ~n~, ~k~ (~1 \le m, n \le 5000~, ~1 \le k \le 10^9~).
~m~ dòng tiếp, mỗi dòng gồm ~n~ số nguyên không âm mô tả bảng ~a~, các số có giá trị không quá ~10^6~.
OUTPUT
Kích thước lớn nhất của bảng vuông thỏa mãn yêu cầu.
SAMPLE INPUT 1
4 4 3
2 7 0 9
2 0 2 3
2 0 0 3
2 0 2 4
SAMPLE OUTPUT 1
2
SUBTASKS
| Subtask | Điểm | Ràng buộc |
|---|---|---|
| 1 | ~300~ | ~n, m \le 100~ |
| 2 | ~700~ | Không có ràng buộc gì thêm. |
duong3982oj Contest 01 - Phần dư và xâu đối xứng
Nộp bàiPoint: 1500
Có ~n~ người tham gia một trò chơi trúng thưởng. Những người này được xếp thành một hàng ngang và được đánh số từ ~1~ đến ~n~. Ban tổ chức sễ thực hiện ~m~ lần quay số, lần thứ ~i~ sẽ quay ra số nguyên dương ~x_i~, số nguyên không âm ~y_i~ và một ký tự ~c_i~. Tất cả những người ở có số thứ tự chia cho ~x_i~ dư ~y_i~ sẽ được Ban tổ chức phát cho một ký tự ~c_i~. Sau khi tất cả các lần quay thưởng được hoàn tất, mỗi người sẽ phải sử dụng những ký tự được phát để tạo thành một xâu đối xứng. Những người thành công tạo được xâu đối xững từ các ký tự được cho sẽ chiến thắng và nhận được số tiền thưởng lớn từ Ban tổ chức.
Bạn được biết các giá trị ~n, m~ và các bộ giá trị ~(x_i, y_i, c_i)~. Hãy xác định xem có bao nhiêu người có thể giành chiến thắng trong trò chơi lần này.
INPUT
Dòng đầu tiên chứa ba số nguyên dương ~n~, ~m~ (~1 \le n, m \le 2 \times 10^5~).
~m~ dòng tiếp, mỗi dòng gồm hai số nguyên không âm ~x_i, y_i~ và một ký tự ~c_i~ thuộc bảng chữ cái tiếng Anh in thường (~1 \le x_i \le n~, ~0 \le y_i \le x_i~).
OUTPUT
Số thứ tự của những người chơi có thể chiến thắng được in theo thứ tự tăng dần.
SAMPLE INPUT 1
5 4
2 1 a
2 0 b
3 2 a
4 2 b
SAMPLE OUTPUT 1
5
Giải thích:
- Các lượt quay thưởng được diễn ra như sau:
| Lượt | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| 1 | a |
|
a |
|
a |
| 2 | |
b |
|
b |
|
| 3 | |
a |
|
|
a |
| 4 | |
b |
|
|
|
- Cả ~5~ người đều có khả năng chiến thắng:
- Người thứ nhất và thứ ba có thể tạo ra xâu
a. - Người thứ tư có thể tạo ra xâu
b. - Người thứ năm có thể tạo ra xâu
aa. - Người thứ hai tạo ra xâu
bab.
- Người thứ nhất và thứ ba có thể tạo ra xâu
SUBTASKS
| Subtask | Điểm | Ràng buộc |
|---|---|---|
| 1 | ~250~ | ~c_i = ~ a. |
| 2 | ~500~ | ~n, m \le 2000~. |
| 3 | ~250~ | ~c_i = ~ a hoặc ~c_i = ~ b. |
| 4 | ~500~ | Không có ràng buộc gì thêm. |
duong3982oj Contest 01 - Cờ "vua"
Nộp bàiPoint: 1750
là một người rất giỏi cờ vua. Sau một thời gian dài tiếp xúc với nó, dường như bắt đầu mất hứng thú với bộ môn này và chuyển sang cờ khác - cờ tướng. Khi tìm hiểu về luật chơi của cờ tướng, rất bất ngờ khi cách đi quân mã ở đây "giống mà khác - khác mà giống" với quân mã ở cờ vua.
Cụ thể hơn, các quân cờ ở cờ tướng được đặt trên những điểm giao của các đường kẻ. Bên cạnh đó, mặc dù quân mã vẫn di chuyển theo hình chữ L giống cờ vua, nhưng chúng không thể đi nếu như có một quân cờ khác chặn ngay trước mặt.
Trong ảnh, quân mã (màu đen) có thể ăn 6 vị trí được đánh dấu tick, nhưng không thể ăn 2 vị trí được đánh dấu X, vì có quân canh (màu đỏ) đang chặn lại.
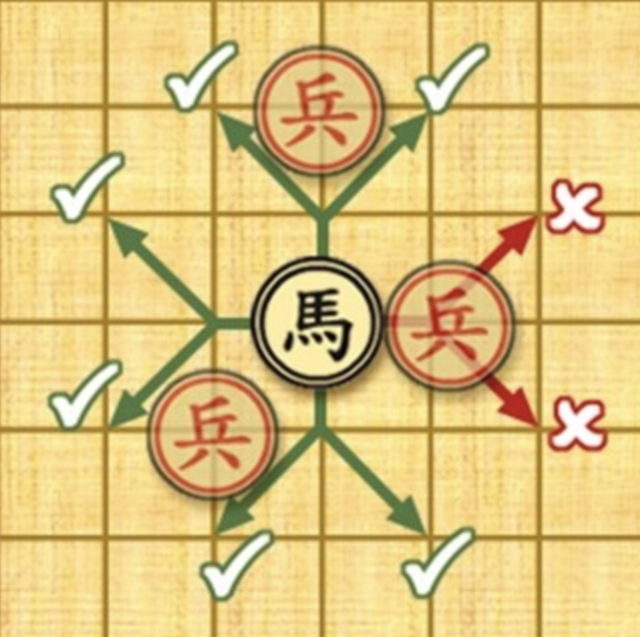
tự hỏi bản thân, có thể đặt tối đa bao nhiêu quân mã trên bàn cờ, và có bao nhiêu cách đặt quân mã thỏa mãn số quân mã trên bàn cờ là nhiều nhất, mà không có hai quân mã nào ăn nhau? Lưu ý, ta không được đặt bất cứ quân cờ nào vào ~q~ ô cấm.
Hai cách đặt được gọi là khác nhau, khi tồn tại một ô (~u~, ~v~) mà có trạng thái (đặt hay không đặt) của ô đó trên hai cách là khác nhau.
INPUT
Dòng đầu chứa hai số nguyên dương ~n~ và ~m~ (~1 \le n \le 5~, ~1 \le m \le 100~) là kích thước của bàn cờ tướng.
Dòng tiếp theo chứa số nguyên ~q~ (~1 \le q \le 200~) là số ô cấm.
~q~ dòng tiếp theo, mỗi dòng là hai số nguyên ~u~, ~v~ (~1 \le u \le n~, ~1 \le v \le m~) là tọa độ của các ô cấm.
OUTPUT
Dòng đầu tiên in ra số quân mã tối đa có thể đặt được.
Dòng thứ hai in ra số cách có thể đặt được số quân mã tối đa, khi chia dư cho ~998244353~.
Nếu chỉ có một output đúng, bạn sẽ nhận được ~250~ điểm mỗi subtasks.
Lưu ý, bạn cần in ra đủ hai số trên hai dòng, nếu không, bạn có thể gặp lỗi Presentation Error.
SAMPLE INPUT 1
4 3
4
1 1
4 3
3 3
2 2
SAMPLE OUTPUT 1
5
2
SUBTASKS
| Subtask | Điểm | Ràng buộc |
|---|---|---|
| 1 | ~500~ | ~n, m \le 3~. |
| 2 | ~500~ | ~q = 0~. |
| 3 | ~750~ | Không có ràng buộc gì thêm. |
duong3982oj Contest 01 - Con đường tình yêu
Nộp bàiPoint: 2000
Cũng trong dịp kỷ niệm 1 năm ngày yêu, đã có một chuyến du lịch cùng với tới quốc gia X.
Quốc gia X có ~n~ thành phố, với ~n - 1~ con đường hai chiều kết nối các thành phố với nhau. Các con đường đảm bảo tính liên thông giữa mọi cặp thành phố trong quốc gia.
Nhằm lên kế hoạch cho chuyến đi, có ~Q~ giả định, mỗi giả định bao gồm hai số nguyên dương ~x~ và ~y~ với ý nghĩa: Nếu quốc gia X xây thêm một con đường (~x, y~), thì sẽ có thêm bao nhiêu cặp thành phố có đường đi ngắn hơn đường đi trên hiện trạng ban đầu của thành phố? Lưu ý, việc thêm một con đường chỉ là giả định, hay các truy vấn chỉ áp dụng lên trạng thái ban đầu của các thành phố.
INPUT
Dòng đầu tiên chứa ba số nguyên dương ~n~, ~q~ (~1 \le n, q \le 10^5~).
~n - 1~ dòng tiếp theo, mỗi dòng bao gồm hai số nguyên dương ~u~ và ~v~ (~1 \le u, v \le n~, ~u \neq v~) thể hiện các con đường.
~q~ dòng tiếp theo, mỗi dòng bao gồm hai số nguyên dương ~x~ và ~y~ (~1 \le x, y \le n~, ~x \neq y~) thể hiện một câu hỏi của .
Vì kinh phí của có hạn, nên tổng khoảng cách từ ~x~ tới ~y~ trên mọi truy vấn sẽ không vượt quá ~5 \times 10^6~.
OUTPUT
In ra ~q~ dòng, mỗi dòng là kết quả của một câu hỏi.
SAMPLE INPUT 1
8 2
1 5
5 2
7 3
3 8
6 4
4 5
6 3
5 7
2 6
SAMPLE OUTPUT 1
10
4
SUBTASKS
| Subtask | Điểm | Ràng buộc |
|---|---|---|
| 1 | ~500~ | ~n, q \le 100~. |
| 2 | ~500~ | Cây có dạng đường thẳng. |
| 3 | ~1000~ | Không có ràng buộc gì thêm. |
duong3982oj Contest 01 - Dãy hình nón
Nộp bàiPoint: 2000
Chắc hẳn, các bạn đều từng nghe đến khái niệm dãy hình nón khi học thuật toán quy hoạch động.
Dãy ~a~ gồm ~n~ phần tử là dãy hình nón khi và chỉ khi tồn tại ~i~ (~1 \le i \le n~) sao cho ~a_1 \le a_2 \le ... \le a_i~ và ~a_i \ge a_{i + 1} \ge ... \ge a_n~.
Tất nhiên, cũng thế và anh ấy rất hứng thú với dãy số này. Vì quá rảnh rỗi sinh nông nỗi, anh ấy quyết định cho bạn bài toán liên quan đến dãy số trên.
Cho mảng ~a~ gồm ~n~ phần tử. muốn chia dãy thành các đoạn liên tiếp và sắp xếp lại sao cho chúng thỏa mãn dãy sau khi sắp xếp lại là một dãy hình nón.
Hỏi cần chia thành ít nhất bao nhiêu đoạn để tạo thành một dãy hình nón?
INPUT
Dòng đầu tiên chứa ba số nguyên dương ~n~ (~1 \le n \le 50~).
Dòng tiếp theo gồm ~n~ số nguyên ~a_i~ (~0 \le a_i \le 10^5~).
OUTPUT
Số đoạn mà cần phải chia.
SAMPLE INPUT 1
6
3 2 1 1 2 3
SAMPLE OUTPUT 1
2
SAMPLE INPUT 2
5
0 1 0 0 0
SAMPLE OUTPUT 2
1
Giải thích:
- Ở ví dụ 1: Đoạn
3 2 1 1 2 3ta chia thành3 2 1 | 1 2 3. Sau đó, ta sẽ sắp xếp thành1 2 3 | 3 2 1. - Ở ví dụ 2: Đoạn
0 1 0 0 0được giữ nguyên do đã thỏa mãn điều kiện đề bài.
SUBTASKS
| Subtask | Điểm | Ràng buộc |
|---|---|---|
| 1 | ~250~ | ~n \le 5~. |
| 2 | ~500~ | ~n \le 20~. |
| 3 | ~500~ | ~a_i \le 1~. |
| 4 | ~750~ | Không có ràng buộc gì thêm. |