Cuội là một dũng sĩ lành nghề. Trong thế giới mà Cuội sinh sống, có tồn tại ~k~ kĩ năng chiến đấu khác nhau được đánh số từ 1 đến ~k~. Ban đầu, Cuội đã thành thạo 4 kĩ năng khác nhau, đó là ~s_1,s_2,s_3~ và ~s_4~.

Cuội lên kế hoạch tấn công một lâu đài chứa chấp các tên tội phạm. May mắn thay, Cuội đã có được thông tin về kiến trúc của lâu đài. Lâu đài bao gồm ~n~ phòng được đánh số từ 1 đến ~n~. Nếu Cuội hiện đang ở phòng thứ ~x~, thì Cuội chỉ có thể ghé thăm phòng ~x+1~, nhưng không thể quay lại phòng ~x-1~.

Có 2 loại phòng là phòng chiến đấu và phòng thư viện. Phòng ~x~ có một trong các thông tin sau:

• ~1\ a~: phòng ~x~ là phòng chiến đấu. Trong căn phòng này có một tên tội phạm mà Cuội có thể chiến đấu. Tên này làm chủ kĩ năng ~a~. Cuội cũng có thể chọn không chiến đấu với tên tội phạm này và ngay lập tức chuyển sang căn phòng tiếp theo.
• ~2~: phòng ~x~ là một thư viện. Trong căn phòng này, Cuội có thể học cách sử dụng một trong những kĩ năng chiến đấu mới, nhưng anh phải quên một kĩ năng mà hiện anh đang làm chủ. Cuội cũng có thể chọn không học gì cả và ngay lập tức chuyển sang phòng tiếp theo.

Khả năng đánh bại tội phạm của Cuội được thể hiện bằng ma trận ~M~. Ma trận ~M~ có kích thước là ~k×k~, trong đó mỗi phần tử có thể là ~0~ hoặc ~1~. Các hàng và cột của ~M~ được đánh số từ ~1~ đến ~k~. Nếu Cuội thành thạo kĩ năng chiến đấu ~i~, thì Cuội có thể đánh bại những tên tội phạm làm chủ kĩ năng chiến đấu ~j~ nếu và chỉ nếu khi hàng ~i~ và cột ~j~ của ma trận ~M~ là ~1~.

Trước khi tấn công lâu đài, Cuội xin lời khuyên của bạn để có thể đánh bại càng nhiều tên tội phạm càng tốt. Hãy giúp Cuội đếm số lượng tội phạm tối đa mà anh ta có thể đánh bại!

Input

• Dòng đầu tiên chứa hai số nguyên ~n,k~ ~(1≤n≤ 2⋅10^5, 4≤ k≤ 20)~
• Dòng hai chứa bốn số ~s_1,s_2,s_3,s_4~ (~1≤s_1,s_2,s_3,s_4≤k~)
• ~k~ dòng tiếp theo, mỗi dòng chứa xâu ~k~ kí tự ~0~ hoặc ~1~ mô tả ma trận ~M~
• Tiếp theo là ~n~ dòng mô tả các phòng trong lâu đài, mỗi dòng theo một trong hai loại sau:
  • ~1\ a~: nếu là phòng chiến đấu (~1≤ a≤ k~)
  • ~2~: nếu là phòng thư viện. Có tối đa 100 phòng là thư viện.

Output

• Đưa ra số tên tội phạm tối đa bị đánh bại.

Subtasks

• ~15\%~ số test không có phòng nào là thư viện
• ~15\%~ số test có số lượng phòng là thư viện ~≤3~
• ~15\%~ số test có ~k=5~
• ~15\%~ số test có ~n≤1000,k≤10~
• ~15\%~ số test có ~n≤1000~
• ~15\%~ số test có ~k≤10~
• ~10\%~ số test còn lại không có ràng buộc gì thêm.

Sample Input

5 5
1 2 3 5
11100
01010
10110
01001
11010
1 2
1 5
2
1 3
1 5

Sample Output

3

Các nhà khoa học đang nghiên cứu về tổ kiển, họ mô phỏng tổ kiến trên một lưới ô vuông n×m bao gồm ~k~ ô ~(x_i,y_i)~. Các ô này có cấu trúc theo dạng cây, hai ô kề cạnh có thể di chuyển qua nhau, hai ô bất kì có thể di chuyển qua lại lẫn nhau thông qua một đường đi duy nhất không lặp lại các ô. Bây giờ các nhà khoa học quan tâm đến việc nếu xét một hình chữ nhật ~(x_1,y_1,x_2,y_2)~ và xem xét các ô thuộc tổ kiến nằm trong hình chữ nhật này thì sẽ có bao nhiêu thành phần liên thông. Các nhà khoa học sẽ xem xét nhiều kịch bản là các hình chữ nhật khác nhau.

Yêu cầu: cho dữ liệu về tổ kiến và ~q~ truy vấn, mỗi truy vấn là một hình chữ nhật, hãy đếm số thành phần liên thông trong hình chữ nhật đó.

Input:

• Dòng đầu chứa hai số nguyên ~n,m~ (~1≤n,m≤2⋅10^5~)
• Dòng thứ hai chứa số nguyên ~k,q~ (~2≤k≤2⋅10^5,1≤q≤2⋅10^5~).
• ~k-1~ dòng tiếp theo, mỗi dòng chứa ~f_i,x_i,y_i~ mô tả ô (~x_i,y_i~) thuộc tổ kiến kết nối với ô (~x_i+1,y_i~ ) nếu ~f_i= h~, hoặc kết nối với ô ~(x_i,y_i+1)~ nếu ~f_i=v~ (~1≤x_i≤n,1≤y_i≤m~). Dữ liệu đảm bảo các ô này tạo thành một cây.
• ~q~ dòng tiếp theo mỗi dòng chứa bốn số ~x_1,y_1,x_2,y_2~ (~1≤x_1≤x_2≤n,1≤y_1≤y_2≤m~). Các ô (~x,y~) được coi là nằm trong hình chữ nhật thỏa mãn ~x_1≤x≤x_2,y_1≤y≤y_2~.

Output:

• Ghi ra ~q~ dòng là kết quả của mỗi truy vấn.

Subtask:

• ~20 \%~ số test có ~n,m,k,q≤100~
• ~20 \%~ số test có ~n,m,k,q≤3000~
• ~30 \%~ số test có ~n,m≤3000,k,q≤10^5~
• ~30 \%~ số test còn lại không có ràng buộc gì thêm.

Sample Input

4 3
8 4
v 1 1
h 1 1
h 2 1
v 2 1
v 2 2
h 1 3
h 3 1
1 1 4 3
3 2 4 3
3 1 3 1
1 2 3 3

Sample Output

1
0
1
2

Cảnh sát đang cần sự giúp đỡ của bạn trong việc tìm kiếm nơi trú ở của một tên tội phạm, kẻ đang ẩn náu ở đâu đó trong thành phố gồm n địa điểm khác nhau, được đánh số từ 1 đến ~n~, và có ~m~ đường hai chiều kết nối hai địa điểm khác nhau.

Thông tin từ các người dân trong thành phố, cảnh sát biết được tên tội phạm đã di chuyển từ một địa điểm ~x~ nào đó để đến nơi trú ẩn ~y~ nào đó. Và các nhân chứng có trông thấy hắn xuất hiện ở ~k~ địa điểm ~u_1,u_2,…,u_k~ trên đường đi từ ~x~ đến ~y~ theo thứ tự nào đó mà cảnh sát chưa xác định. Lưu ý rằng tên tội phạm có thể di chuyển từ ~x~ đến ~y~ thông qua các địa điểm khác không có trong ~k~ địa điểm mà các nhân chứng trông thấy. Tuy nhiên, cảnh sát đã phân tích đặc điểm của tên tội phạm này và biết rằng hắn sẽ luôn di chuyển theo đường đi ngắn nhất giữa hai địa điểm ~x~ và ~y~.

Nhiệm vụ của bạn là tìm các địa điểm có thể là ~y~ để giúp cảnh sát có thể nhanh chóng tìm được hắn. Tất nhiên, có thể lời khai của các nhân chứng không đồng nhất dẫn đến không tìm thấy một địa điểm ~y~ nào thỏa mãn.

Input:

• Dòng đầu chứa số nguyên ~n,m,k~ (~1≤k≤n≤2⋅10^5,1≤m≤2⋅10^5~)
• Dòng thứ hai chứa ~k~ số nguyên ~u_i~ mô tả những địa điểm tên tội phạm đi qua (~1≤u_i≤n~)
• ~m~ dòng tiếp theo, mỗi dòng chứa ba số nguyên ~a,b,c~ mô tả có đường nối trực tiếp giữa hai địa điểm ~a~ và ~b~ có độ dài là ~c~ (~1≤a≠b≤n,1≤c≤10^9~)

Output:

• Dòng đầu ghi ra số ~p~ là số địa điểm có thể là ~y~
• Dòng thứ hai ghi ra ~p~ số nguyên là những địa điểm có thể là ~y~ theo thứ tự tăng dần.

Subtasks:

• ~15 \%~ số test có ~m=n-1~, và mỗi địa điểm được kết nối trực tiếp với tối đa 2 địa điểm khác.
• ~15 \%~ số test có ~m=n-1~
• ~15 \%~ số test có ~n,m≤100~
• ~15 \%~ số test có ~n,m≤1000~
• ~20 \%~ số test có ~k≤5~
• ~20 \%~ số test còn lại không có ràng buộc gì thêm

Sample Input:

6 6 2
1 5
1 2 1
2 3 1
3 4 1
4 5 1
5 6 1
6 1 1

Sample Output:

4
1 2 4 5

Cho hai số nguyên dương ~L,R~. Hãy đếm xem có bao nhiêu số nguyên dương ~x~ thuộc đoạn [~L,R~] chia hết cho ~19~; sao cho ở dạng biểu diễn thập phân, ~x~ không chứa hai chữ số nào có tổng chia hết cho ~3~.

Input:

• Dòng đầu chứa số nguyên dương ~T~ là số lượng testcase (~1 ≤ T ≤ 10^5~);
• Mỗi test được mô tả trên hai dòng là ~L~ và ~R~ (~1 ≤ L ≤ R ≤ 10^{10000}~).

Output:

• Với mỗi testcase, ghi trên một dòng số lượng số nguyên dương ~x~ tìm được, sau khi chia lấy dư cho ~1000000007~

Subtasks:

• Có ~50 \%~ số test với ~R ≤ 10^6~;
• Có ~30\%~ số test với tổng độ dài của tất cả các số ~R~ trong ~T~ testcase không vượt quá ~10^3~;
• Có ~20 \%~ số test với ràng buộc gốc.

Sample Input:

2
1 100
101 200

Sample Output:

4
2

Giải thích:

• Các số thỏa mãn testcase 1 là: ~19, 38, 76, 95~.

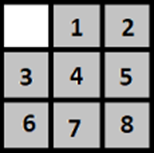
Xếp hình là một trong những trò kinh điển thời tuổi thơ dữ dội của chúng ta. Trò chơi gồm một bảng ~3 × 3~ chứa 8 miếng ghép và một ô trống. Người chơi cố gắng sắp xếp lại các miếng ghép thành một thứ tự định sẵn, bằng cách lặp lại việc di chuyển một trong các miếng ghép kề cạnh với ô trống vào ô trống (và dĩ nhiên ô trống sẽ chuyển sang vị trí của miếng ghép). Để đơn giản, các miếng ghép được đánh số từ 1 đến 8 và thứ tự định sẵn được cho trong hình sau:

Ở phiên bản khó của trò chơi, bạn cần tìm số bước di chuyển ít nhất để đưa trạng thái đã cho về trạng thái định sẵn. Hùng đã chơi trò này nhiều lần nhưng vẫn gặp vấn đề với phiên bản khó, và có vẻ bài tập này được thiết kế để dành riêng cho cậu.

Input:

• Dòng đầu chứa số nguyên dương ~T~ là số lượng testcase;
• ~T~ dòng tiếp theo mỗi dòng chứa 9 số nguyên là một hoán vị của ~0, 1, 2, . . . , 8~ mô tả một trạng thái bắt đầu. Các số trong hoán vị lần lượt là các số ghi trên các ô của bảng, theo thứ tự từ trái sang phải, từ trên xuống dưới. Số 0 đại diện cho ô trống.

Output;

• Gồm ~T~ dòng, mỗi dòng ghi một số nguyên là số bước di chuyển ít nhất, hoặc -1 nếu không thể đưa trạng thái này về trạng thái định sẵn.

Subtasks:

• Trong tất cả các test: ~T ≤ 10^6~;
• ~30 \%~ test với ~T = 5~ và kết quả không vượt quá 10;
• ~30 \%~ test tiếp theo có kết quả không vượt quá 10;
• ~40 \%~ test tiếp theo với ràng buộc gốc.

Sample Input:

4 
0 1 2 3 4 5 6 7 8 
3 1 2 0 4 5 6 7 8 
1 2 3 4 5 6 7 8 0 
2 3 0 4 1 5 8 6 7

Sample Output:

0 
1 
22 
-1

Vương quốc có ~n~ thành phố và ~n-1~ con đường hai chiều, đảm bảo đi lại giữa mọi cặp thành phố. Thành phố x được gọi là quản lý ~y~ nếu ~x~ nằm trên đường đi đơn từ ~y~ đến 1. Sản lượng lương thực tại thành phố ~x~ là ~w_x~. Quốc vương muốn chọn ra một đỉnh để xây dựng kho dự trữ, chi phí vận chuyển lương thực nếu xây dựng kho dự trữ tại ~u~ là ~∑_{v=1}^n {w_v×d(v,u)}~ với ~d(v,u)~ là số cạnh trên đường đi đơn từ ~v~ đến ~u~.

Có ~Q~ thay đổi cho sản lượng được báo cáo, mỗi thay đổi có dạng ~1\ u\ c~ hoặc ~2\ u\ c~ tương ứng là tăng ~w_u~ lên ~c~ đơn vị hoặc tăng ~w_v~ lên ~c~ đơn vị với mọi ~v~ quản lý bởi ~u~. Sau mỗi thay đổi, cần tìm đỉnh ~u~ để xây dựng kho dữ trữ sao cho tổng chi phí vận chuyển lương thực là nhỏ nhất, nếu có nhiều ~u~ như vậy thì chọn ~u~ nhỏ nhất.

Input:

• Dòng đầu chứa hai số nguyên dương ~n~ và ~Q~;
• Dòng thứ hai chứa ~n~ số ~w_1,w_2,...,w_n~;
• Mỗi dòng trong số ~n - 1~ dòng tiếp theo chứa hai số ~u\ v~ mô tả một cạnh của cây;
• Mỗi dòng trong số ~Q~ dòng tiếp theo chứa ba số ~t\ u\ c~ mô tả một thay đổi

Output:

• Ghi ~Q~ dòng là chỉ số của đỉnh được chọn sau thay đổi thứ ~Q~.

Subtasks:

• Trong tất cả các test: ~n,Q ≤ 10^5; 1 ≤ w_i ≤ 10^6; |c| ≤ 10^6.~
• Có ~12 \%~ số test với ~n,Q ≤ 5000~;
• Có ~16 \%~ số test có cạnh nối từ ~x~ đến ~x - 1~ với mọi ~2 ≤ x ≤ n;~
• Có ~16 \%~ số test có cạnh nối từ ~x~ đến ~[x/2]~ với mọi ~2 ≤ x ≤ n;~
• Có ~20 \%~ số test không có thay đổi loại 2;
• Có ~36 \%~ số test với ràng buộc gốc.

Sample Input:

5 3 
1 3 2 1 4 
1 2 
1 3 
2 4 
2 5 
1 2 2 
2 3 4 
1 1 5

Sample Output:

2 
2 
1