Bạn được cho 1 dãy ~A~ gồm ~n~ số nguyên dương ~A_1, A_2, ..., A_n~ và dãy ~B~ gồm ~m~ số nguyên dương ~B_1, B_2, ... B_m~ và một số ~k~

Một cặp số ~(i,j)~ được gọi là tốt nếu như ~A_i~ ~\vdots~ ~(~ ~B_j \times k~ ~)~ với ~\vdots~ là kí hiệu chia hết

Hãy tìm số lượng của các cặp tốt

Input

Dòng đầu là số nguyên dương ~n~, ~m~ và ~k~ ~(1 \le n,m \le 10^5 , 1 \le k \le 10^3)~.

Dòng tiếp theo là ~n~ số nguyên dương ~A_i~ ~(1 \le A_i \le 10^6 )~

Dòng tiếp theo là ~m~ số nguyên dương ~B_i~ ~(1\le B_i \le 10^6)~

Output

Một dòng duy nhất là số lượng các cặp tốt

Sample Input

3 3 1
1 3 4 
1 3 4

Sample Output

5

Dãy số ~a_1, a_2,..., a_n~ được gọi là tăng nếu ~a_1 < a_2 < … < a_n~.

Bạn được cho một dãy số ~b_1, b_2,..., b_n~ và một số nguyên dương ~d~. Trong mỗi lần thao tác, bạn chọn một phần tử của dãy số và cộng thêm ~d~ vào nó. Số thao tác ít nhất là bao nhiêu để biến đổi dãy số đã cho trở thành dãy số tăng.

Input

Dòng đầu tiên là số nguyên ~n~ và ~d~ ~(1 \le n \le 10^6, 1 \le d \le 10^9)~

Dòng tiếp theo là ~n~ số nguyên ~b_i~ ~(1 \le b_i \le 10^9 )~

Output

In ra một dòng duy nhất là số thao tác tối thiểu để biến đổi dãy số đã cho trở thành dãy số tăng.

Sample Input

4 2
1 3 3 2

Sample Output

3

Giải thích

dãy ~b=[1, 3, 3, 2]~ và ~d = 2~. Số thao tác ít nhất để biến đổi dãy số trở thành dãy số tăng là 3 và một trong các cách thực hiện như sau:

• Thao tác 1: cộng thêm ~d~ vào phần tử thứ ba, dãy trở thành ~[1,3, 5, 2]~
• Thao tác 2: cộng thêm ~d~ vào phần từ thứ tư, dãy trở thành ~[1,3, 5, 4]~
• Thao tác 3: cộng thêm ~d~ vào phần từ thứ tư, dãy trở thành ~[1,3, 5, 6]~ và là dãy số tăng.

~Zinno~ đang chơi trò tiêu diệt quái vật với mục tiêu tiêu diệt càng nhiều quái vật càng tốt. Có tổng cộng ~n~ quái vật, mỗi quái vật thứ ~i~ có sức mạnh phòng thủ là ~a_i~ ~\forall i \in [1,n]~. ~Zinno~ có một đội gồm ~m~ anh hùng, mỗi anh hùng có sức mạnh ~b_j~ ~\forall j \in [1,m]~.

Một anh hùng có thể tiêu diệt một quái vật nếu sức mạnh của anh hùng đó lớn hơn hoặc bằng sức mạnh phòng thủ của quái vật, tức là ~b_j \geq a_i~. Mỗi anh hùng chỉ có thể tiêu diệt một quái vật duy nhất.

~Zinno~ có ~k~ đồng tiền, mỗi đồng tiền cho phép tăng sức mạnh của một anh hùng thêm ~x~ đơn vị. Tuy nhiên, mỗi anh hùng chỉ có thể nâng cấp một lần duy nhất.

Câu hỏi đặt ra là: Số lượng quái vật tối đa mà ~Zinno~ có thể tiêu diệt là bao nhiêu?

Input

Dòng đầu tiên gồm các số nguyên ~n~, ~m~, ~k~ , ~x~ ~(1 \le n,m \le 5 \times 10^4,0 \le k \le m, 0 \le x \le 10^9 )~

Dòng thứ hai là ~n~ số nguyên ~a_i~ ~(0 \le a_i \le 10^9)~

Dòng thứ ba là ~m~ số nguyên ~b_j~ ~(0 \le b_j \le 10^9)~

Output

Một dòng duy nhất là số lượng quái tối đa mà anh có thể giết

Sample Input

3 5 3 10
10 15 30
0 10 10 10 10 

Sample Output

2

Giải thích

Ta sẽ sử dụng ~1~ đồng lên anh hùng ~j=2~ và đi đánh quái ~i=2~ ~(10+10 \geq 15)~

Ta cho anh hùng ~j=3~ đi đánh quái ~i=1~ ~(10 \geq 10)~

Sau đó dù ta dùng tiền mua tăng sức mạnh cho bất cứ anh hùng nào cũng không thể đi tiêu diệt thêm quái nữa

Trong một vương quốc xa xôi,có ~n+1~ thành phố được đánh số từ ~0~ đến ~n~ , kết nối với nhau bởi một mạng lưới gồm ~n~ con đường, mỗi thành phố không thể đi về lại chính thành phố mình nếu không đi về bằng các con đường đã đi.

Một ngày nọ, tổ chức Sariella, một tổ chức bí ẩn và đầy quyền lực, đã phát triển một loại Virus kỳ lạ với khả năng lây lan đặc biệt và nguy hiểm. Virus này có cơ chế lây nhiễm vô cùng phức tạp và khó lường, khiến cho việc kiểm soát và ngăn chặn trở nên vô cùng khó khăn.

Cơ chế lây nhiễm của Virus này được mô tả như sau:

Ở ngày thành phố ~i~

• Nếu một thành phố kề nó nhiễm bệnh vào ngày ~x-1~, thì vào ngày ~x~, Virus sẽ lây lan sang các thành phố ~i~ nếu ~i~ là lẻ.

• Nếu một thành phố bị nhiễm bệnh vào ngày ~x-2~,thì vào ngày ~x~, Virus sẽ tiếp tục lây lan sang các thành phố ~i~ nếu ~i~ là chẵn.

Quá trình này cứ tiếp diễn, tạo nên một chuỗi lây nhiễm liên tục và không ngừng nghỉ, như một cơn bão không thể kiểm soát.

Ban đầu, mỗi thành phố trong vương quốc sẽ bị nhiễm các loại Virus khác nhau,nhưng cơ chế lây lan lại giống nhau,mỗi Virus lây lan độc lập với nhau

Hỏi với mỗi thành phố, Virus bắt đầu ở thành phố ~i~ cần bao nhiêu ngày để lây nhiễu hết vương quốc.

Input

Dòng đầu là số nguyên ~n~ ~(2 \le n \le 10^6)~

~n~ dòng tiếp theo,mỗi dòng gồm 2 số nguyên ~u~ và ~v~,thể hiện thành phố ~u~ và ~v~ có ~1~ con đường đi qua nhau ~(0 \le u,v \le n)~

Output

Một dòng duy nhất có ~n+1~ số nguyên dương,số thứ ~i~ là thời gian cần để viruss bắt đầu từ thành phố ~i~ cố thể lây lan hết vương quốc

Sample Input

4
0 1
0 2
2 3
2 4

Sample Output

4 6 3 5 5

Giải thích

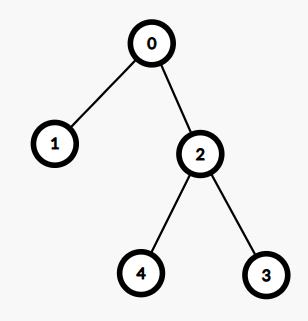
Ở thành phố ~i=0~:

• Thành phố ~1~ bị nhiễm ở ngày thứ nhất
• Thành phố ~2~ bị nhiễm ở ngày thứ hai
• Thành phố ~3~ bị nhiễm ở ngày thứ ba
• Thành phố ~4~ bị nhiễm ở ngày thứ tư

Ở thành phố ~i=1~:

• Thành phố ~0~ bị nhiễm ở ngày thứ ~2~
• Thành phố ~2~ bị nhiễm ở ngày thứ ~4~
• Thành phố ~3~ bị nhiễm ở ngày thứ ~5~
• Thành phố ~4~ bị nhiễm ở ngày thứ ~6~

Ở thành phố ~i=2~:

• Thành phố ~3~ bị nhiễm ở ngày thứ nhất
• Thành phố ~0~ và ~4~ bị nhiễm ở ngày thứ hai
• Thành phố ~1~ bị nhiễm ở ngày thứ ba

Ở thành phố ~i=3~:

• Thành phố ~2~ bị nhiễm ở ngày thứ ~2~
• Thành phố ~0~ và ~4~ bị nhiễm ở ngày thứ ~4~
• Thành phố ~1~ bị nhiễm ở ngày thứ ~1~

Ở thành phố ~i=4~:

• Thành phố ~2~ bị nhiễm ở ngày thứ ~2~
• Thành phố ~3~ bị nhiễm ở ngày thứ ~3~
• Thành phố ~0~ bị nhiễm ở ngày thứ ~4~
• Thành phố ~1~ bị nhiễm ở ngày thứ ~5~

Có một lưới thành phố kích thước ~n \times m~, mỗi thành phố được kết nối bởi các con đường một chiều, biểu diễn trong một ma trận ~n \times m~ như sau:

• >: Đường đi sang phải, nghĩa là từ thành phố ~(i,j)~ chỉ có thể đi đến thành phố ~(i,j+1)~.

• <: Đường đi sang trái, nghĩa là từ thành phố ~(i,j)~ chỉ có thể đi đến thành phố ~(i,j-1)~.

• ^: Đường đi lên trên, nghĩa là từ thành phố ~(i,j)~ chỉ có thể đi đến thành phố ~(i-1,j)~.

• v: Đường đi xuống dưới, nghĩa là từ thành phố ~(i,j)~ chỉ có thể đi đến thành phố ~(i+1,j)~.

~Zinno~ muốn đi từ ô ~(1,1)~ đến ô ~(n,m)~, anh ấy chỉ có thể đi theo các con đường một chiều đã có sẵn. Tuy nhiên, có thể các con đường một chiều này có thể không cho phép anh ấy đi từ ô ~(1,1)~ đến ô ~(n,m)~. Vì vậy, ~Zinno~ có thể thay đổi hướng của một số con đường để tìm được đường đi, nhưng anh ấy chỉ có thể thay đổi hướng của con đường tại một thành phố duy nhất mỗi lần.

Câu hỏi là: ~Zinno~ có cần thay đổi hướng của bất kỳ con đường nào không? Nếu có, cần thay đổi tại bao nhiêu thành phố?

Input

Dòng đầu tiên là 2 số nguyên ~n~ và ~m~ ~(1 \le n,m \le 1000, n \times m \le 2 \times 10^5)~

~n~ dòng tiếp theo,mỗi dòng là ~1~ xâu gồm ~m~ kí tự chỉ bao gồm > , < , ^ , v

Output

Dòng đầu tiên in ra YES nếu cần thay đổi,NO nếu không

In ra dòng tiếp theo nếu dòng trên là YES, số lượng thành phố cần thay đổi đường

Sample Input

4 4
>>>>
<<<<
>>>>
<<<<

Sample Output

YES
3

Giải thích

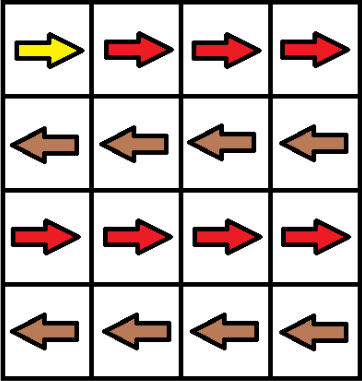
Thay đổi ô ~(1,4)~ thành v,thay đổi ô ~(2,1)~ thành v,thay đổi ô ~(3,4)~ thành v

Một ngày nọ, trong một vương quốc xa xôi, có một đội phiêu lưu gồm ~n~ các anh hùng, mỗi người mang trong mình một sức mạnh đặc biệt, được đại diện bởi hai chỉ số: sức mạnh và khả năng phép thuật. Mỗi anh hùng đã sẵn sàng để thực hiện một nhiệm vụ bảo vệ vương quốc khỏi mối đe dọa của những kẻ xấu xa.

Vua của vương quốc, người đã thu thập rất nhiều thông tin về các anh hùng, có trong tay danh sách chỉ số sức mạnh và khả năng phép thuật của các anh hùng. Ngoài ra, vua còn có một danh sách gồm ~Q~ yêu cầu, nơi mỗi yêu cầu mô tả điều kiện cần để chọn một anh hùng tham gia nhiệm vụ sắp tới.

Trong một yêu cầu, vua cần tìm giá trị tối đa của tổng sức mạnh và khả năng phép thuật của một anh hùng, với điều kiện sức mạnh của anh hùng đó phải lớn hơn hoặc bằng ~x~ và khả năng phép thuật phải lớn hơn hoặc bằng ~y~ . Nếu thoả mãn nhà vua sẽ ghi tổng chỉ số sức mạnh và khả năng phép thuật vào yêu cầu đó, ngược lại vua sẽ ghi là -1

Input

Dòng đầu tiên là số nguyên ~n~ và ~Q~ ~(1 \le n \le 10^5 , 0 \le Q \le 10^5 )~

Dòng thứ hai là ~n~ số nguyên dương ~A_i~ ~(1 \le A_i \le 10^9)~ ~-~ là chỉ số sức mạnh của các anh hùng

Dòng thứ ba là ~n~ số nguyên dương ~B_i~ ~(1 \le B_i \le 10^9)~ ~-~ là chỉ số phép thuật của các anh hùng

~Q~ dòng tiếp theo,dòng thứ ~i~ là 2 số nguyên ~x~ và ~y~ ~(1 \le x,y \le 10^9)~ ~-~ yêu cầu về sức mạnh và phép thuật theo yêu cầu của nhà vua

Output

In ra ~Q~ dòng,dòng thứ ~i~ là đáp án cho yêu cầu của nhà vua

Sample Input

4 3
4 3 1 2
2 4 9 5
4 1
1 3 
2 5

Sample Output

6
10 
7

Giải thích

Đối với truy vấn đầu tiên ~[4, 1]~, anh hùng ở chỉ số ~j = 1~ thỏa mãn điều kiện với tổng là ~6~.

Đối với truy vấn thứ hai ~[1, 3]~, anh hùng ở chỉ số ~j = 3~ thỏa mãn điều kiện với tổng là ~10~.

Đối với truy vấn thứ ba ~[2, 5]~, anh hùng ở chỉ số ~j = 4~ thỏa mãn điều kiện với tổng là ~7~.

~Nana~ và ~Zinno~ đang tham gia vào một cuộc phiêu lưu hấp dẫn trong trò chơi MMORPG. Hôm nay, họ có nhiệm vụ thám hiểm một hầm ngục bí ẩn với cấu trúc đặc biệt. Nhiệm vụ của họ không giống nhau:

• ~Nana~: Bắt đầu từ tầng ~1~ và thu thập điểm kinh nghiệm nhiều nhất có thể. Cô sẽ di chuyển đến các tầng liên kết và tiếp tục cho đến khi không thể đi tiếp nữa.

• ~Zinno~: Bị dịch chuyển vào một tầng ngẫu nhiên ~z~, ~Zinno~ phải tìm đường nhanh nhất về tầng ~1~ để hoàn thành nhiệm vụ.

Tuy nhiệm vụ khác nhau nhưng họ lại cùng làm nhiệm vụ trên môt hầm ngục,với cấu trúc như sau:

• Hầm ngục này có ~n~ tầng và ~n-1~ cầu thang, tạo thành một cấu trúc giống như đồ thị cây.
• Các tầng được kết nối với nhau thông qua các cầu thang, mỗi cầu thang nối hai tầng lại với nhau.
• Mỗi tầng có thể liên kết với nhiều tầng khác thông qua cầu thang, nhưng không có chu kỳ, tức là không có đường nào quay lại chính nó.

Dưới đây là một số quy tắc đặt ra của cả hai nhiệm vụ là như sau:

• Điểm kinh nghiệm: Mỗi lần ~Nana~ hoặc ~Zinno~ đi vào tầng ~i~, họ sẽ nhận hoặc mất một lượng điểm kinh nghiệm ~exp_i~, nếu ~exp_i~ ~>~ 0 thì đó là điểm kinh nghiệm họ nhận được, ngược lại ~exp_i~ ~<~ 0 thì đó là số kinh nghiệm cần trả của tầng đó. Nếu một tầng đã có người nhận hoặc trả điểm kinh nghiệm, người đến sau sẽ không nhận hoặc phải trả nữa.

• Chia sẻ điểm kinh nghiệm: Nếu cả hai cùng đến một tầng, điểm kinh nghiệm sẽ được chia đều, cụ thể là mỗi người được nhận ~\lfloor \frac{exp_i}{2} \rfloor~.

• Không quay lại: Cả ~Nana~ và ~Zinno~ không thể quay lại các tầng đã đi qua.

~Zinno~ không quan tâm điến điểm kinh nghiệm mà chỉ cần hoàn thành nhiệm vụ,còn ~Nana~ thì muốn điểm kinh nghiệm là lớn nhất có thể.

Bạn hãy xác định xem ~Nana~ có tối đa bao nhiêu điểm kinh nghiệm

Input

Dòng đầu tiên là 2 số nguyên dương ~n,q~ ~(2 \le n,q \le 10^5, 2 \le z \le n )~

Dòng tiếp theo gồm ~n~ số nguyên ~exp_i~ ~-~ là điểm kinh nghiệm của cửa tầng đó ~(-10^9 \le exp_i \le 10^9)~

~n-1~ dòng cuối, mỗi dòng gồm ~2~ số nguyên dương ~u,v~ ~(u \neq v , 1 \le u,v \le n)~ ~-~ thể hiện có cầu thang nối giữa tầng ~u~ và ~v~

Output

In ra số điểm kinh nghiệm tối đa mà ~Nana~ nhận được

Sample Input

5 4
-2 4 2 -4 6
1 2
2 3
2 4
4 5

Output

6

Giải thích

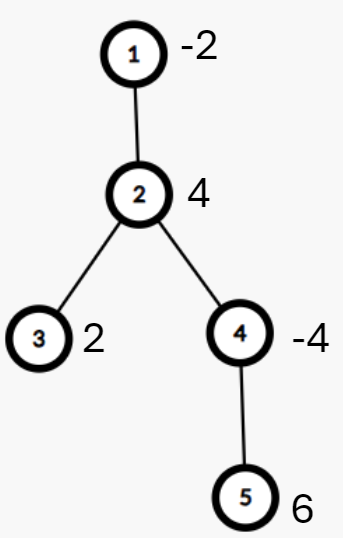
Như hình trên:

-Ban đầu ~Nana~ ở tầng ~1~, ~Zinno~ ở tầng ~4~. Họ phải trả điểm kinh nghiệm của các tầng tương ứng của họ.

Điểm kinh nghiệm của ~Nana~ bây giờ là ~-2~.

• Cả ~Nana~ và ~Zinno~ đều di chuyển đến tầng ~2~. Vì họ đến đây cùng lúc, nên họ cùng mở tầng đó và chia sẻ điểm.

  Điểm kinh nghiệm của ~Nana~ trở thành ~-2 + \frac{4}{2}~ ~= 0~.

• ~Nana~ di chuyển đến tầng ~4~. Vì ~Zinno~ đã trả điểm của tầng này, nên thu nhập của ~Nana~ không đổi.

  ~Zinno~ di chuyển đến tầng ~1~ và dừng lại.

• ~Nana~ di chuyển đến tầng ~5~ và mở cổng ở đó. Điểm kinh nghiệm của cô ấy trở thành ~0 + 6 = 6~.